Päiväkirja
8.3.2025
Tein p5.js:llä tommosen simppelin pasianssin. Pelin ideana on että sekoitetaan pakka ja nostetaan pakasta kortti kerrallaan ja samalla lasketaan neljä kertaa yhdestä kolmeentoista. Peli päättyy jos nostetun kortin silmäluku on sama kuin laskettu luku, esimerkiksi ässä kun lasketaan yksi, tai kunkku kun lasketaan 13.
Pelin koodiin on lisätty testausominaisuus, millä pakka järjestetään semmoiseen asentoon että peli menee takuuvarmasti läpi. Käytännössä riittää kun maittain järjestetystä pakasta siirretään päällimmäinen kortti pohjalle. Normaalistikin pelaten olen saanut pelin loppuun useamman kerran.
Millä todennäköisyydellä pasianssin saa pelattua loppuun? Koitin laskea tätä analyyttisesti, mutta en keksinyt ratkaisua. Toinen vaihtis on simuloida peliä monte carlolla. Toistetaan peliä vaikka yhdestä kymmeneen tuhanteen kertaan ja lasketaan mikä osuus peleistä menee läpi. Tämän pitäisi konvergoitua melko nopeasti oikeaa tn:ää kohti.
Alla on R-koodi monte carlo-simulaatioon.
kortit <- rep(c(1:13), 4)
pelaa <- function() {
sekotus <- sample(kortit)
kusi <- any(sekotus == kortit)
! kusi
}
toista <- function(n) {
tulos <- replicate(n, pelaa())
läpi <- sum(tulos)
läpi / n
}
toistot <- sapply(seq_len(10000), toista)
plot(
x = 1:length(toistot),
y = toistot,
type = 'l',
col = 'red',
xlab = 'toistot',
ylab = 'tn(peli läpi)',
main = 'Pöliän sian pasianssi'
)
round(100 * mean(toistot), digits = 2)
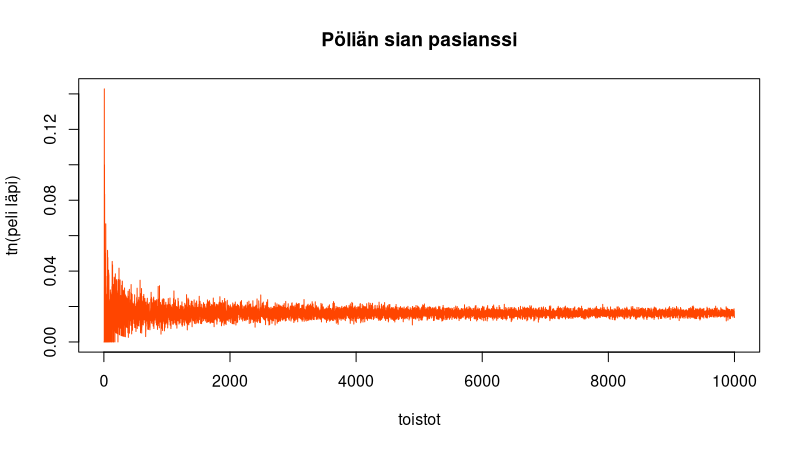
Läpipeluun todennäköisyys on arviolta 1,62% eli sadasta pelikerrasta keskimäärin 1-2 menee läpi.